Continuum mechanics (fluid-structure interaction, anisotropy, incompressibility, plasticity)
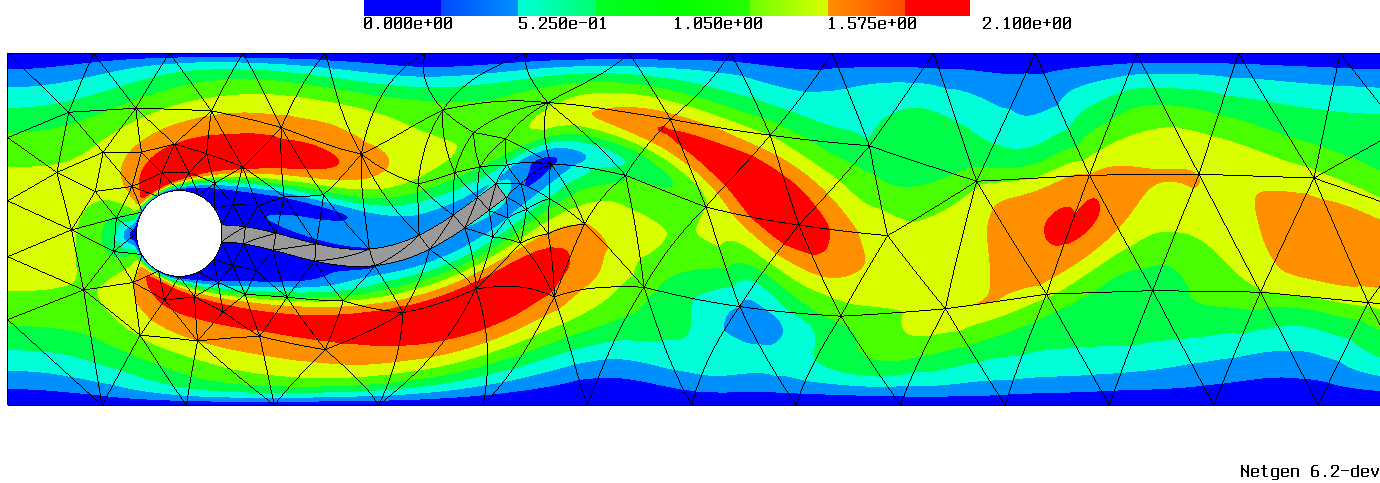
The interaction between fluids and solids can be demanding due to the permanent change of the material domains. We investigated Arbitrary Lagrangian-Eulerian (ALE) methods, where the fluid velocity gets discretized by exactly divergence-free finite elements. We derived a method where the incompressibility constraint is exactly fulfilled for moving domains [2017, 2021].
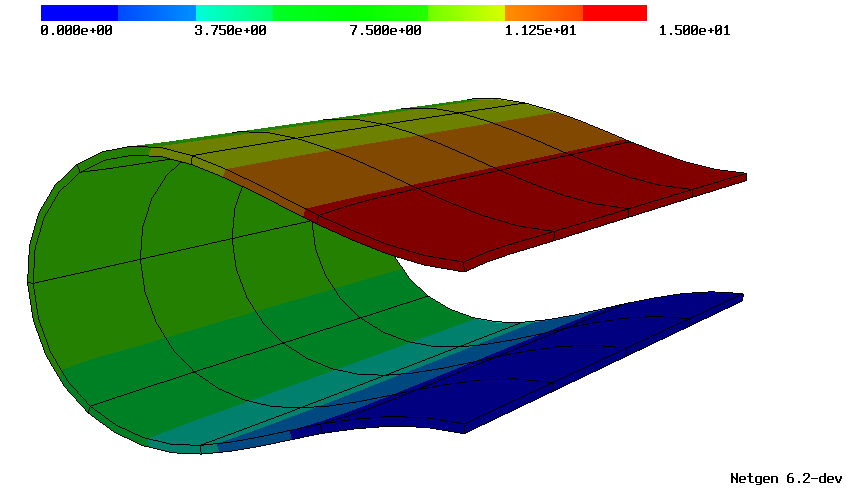
For anisotropic physical structures, shear locking can be observed in the finite element discretization of (nonlinear) elasticity. The tangential displacement and normal-normal-stress continuous (TDNNS) method has elegantly circumvented this behaviour in linear elasticity. Besides the displacement, the stress tensor is introduced as an additional variable. The stress and displacement fields are discretized by matrix- and vector-valued finite elements, where only specific components are continuous. Extending this mixed method to the finite strain regime turned out to be challenging as, on the one hand, this two-field formulation would require inverting the nonlinear stress-strain relation, and on the other hand, the displacement’s weak regularity leads to a distributional gradient, which cannot be multiplied in general. We were able to solve this problem in terms of a three-field Hu–Washizu formulation by computing a discrete \(L^2\) Riesz representative of the distributional deformation gradient as a third field [2021, 2021]. The resulting method extends the robustness property concerning shear locking to the nonlinear regime.
Real-life materials cannot be indefinitely deformed without damaging them. Plasticity involves irreversible deformations, and damage weakens the material structure. We investigated a novel finite-strain model including plasticity and damage in two and three spatial dimensions numerically and theoretically [2021].
Rubber-like materials entail difficulties in numerical simulations due to their (nearly) incompressible character. We investigated under which boundary conditions a divergence-free displacement can be determined independently from the pressure reaction in incompressible linear elasticity. If not possible, we derived conditions under which it is possible to determine the displacement pressure robustly, i.e. pollution-free from the pressure reaction [2023]. The mass-converging mixed stress (MCS) method has been developed to simulate the (Navier-)Stokes equations in a pressure robust manner. It can be readily adapted to solve (nearly) incompressible linear elasticity problems. However, similar to the TDNNS method, it relies on the inversion of the material law. This makes incompressible finite elasticity unfeasible. We used a three-field Hu–Washizu formulation and a stabilization motivated by hybrid Discontinuous Galerkin (HDG) methods to successfully extend the MCS method to the nonlinear regime by adding the deformation gradient as an additional strain unknown [2025].
