Shape optimization
In several problems in industry and medicine, including the optimal design of aircraft, electric motors, or electric impedance tomography, an optimal shape with respect to a given objective function under constraints is searched for. Shape optimization problems involve the shape derivative of possibly lengthy and complicated expressions. We implemented an automated shape differentiation tool in the open-source finite element software NGSolve, enabling shape gradient and shape Newton methods without the need to compute the shape derivative by hand [2021]. In addition, this makes using non-Lagrangian finite elements in shape optimization problems more attractive, where additional space-dependent transformation rules have to be differentiated.
 |  |
| Initial and optimized geometry of a cantilever under vertical force on the right side using a St. Venant–Kirchhoff model in nonlinear elasticity. | |
We have successfully applied this framework to minimize the Canham–Helfrich–Evans (CHE) bending energy in the context of cell membranes [2023]. The method used to reduce the fourth-order problem to a mixed second-order problem turned out to be fruitful in combination with the theory of shape optimization.
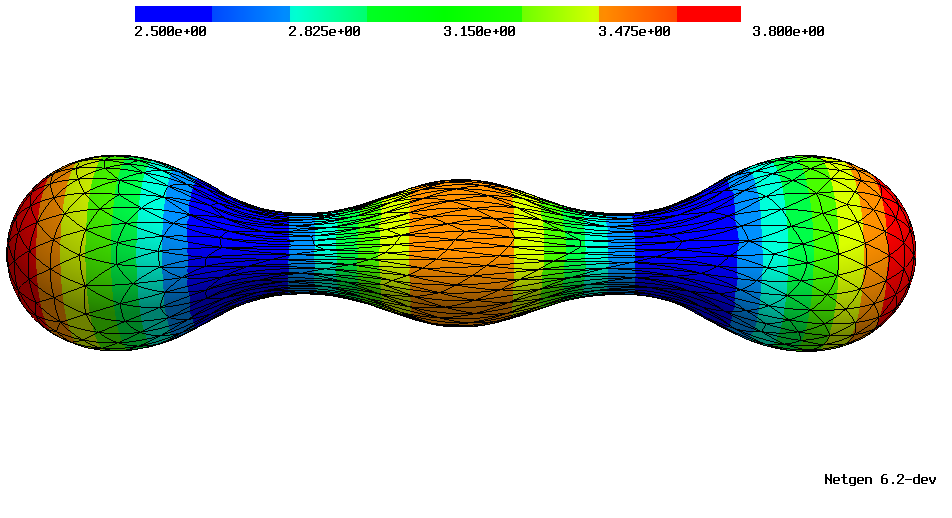 | 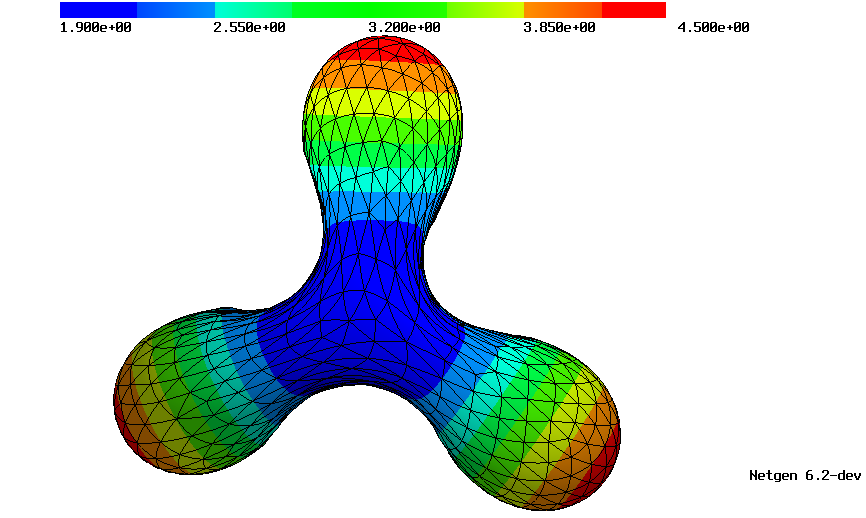 |
| Two solutions of the CHE energy with different nonzero spontaneous curvatures. Colors indicate the modulus of the mean curvature of the shapes. | |
