Nonlinear shell analysis

To simulate thin-walled structures, where one direction is significantly smaller than the others, a dimension reduction leads to surface shell equations. Shells have a wide range of industrial applications and are an active research field. Their numerical solution with the finite element method is essential. Motivated by discrete differential geometry we used a distributional Weingarten tensor acting on Hellan–Herrmann–Johnson finite elements, we developed locking-free mixed finite element methods for nonlinear Koiter shells [2019, 2021, 2024] and extended the tangential-displacement and normal-normal stress continuous (TDNNS) method from linear Reissner–Mindlin plates to nonlinear Naghdi shells [2024]. With the structure-preserving finite elements, our methods can handle non-smooth shell structures such as kinked and branched shells.

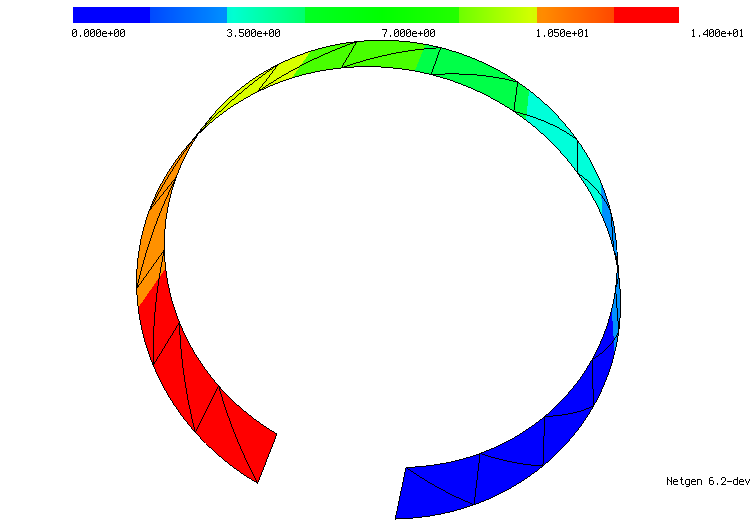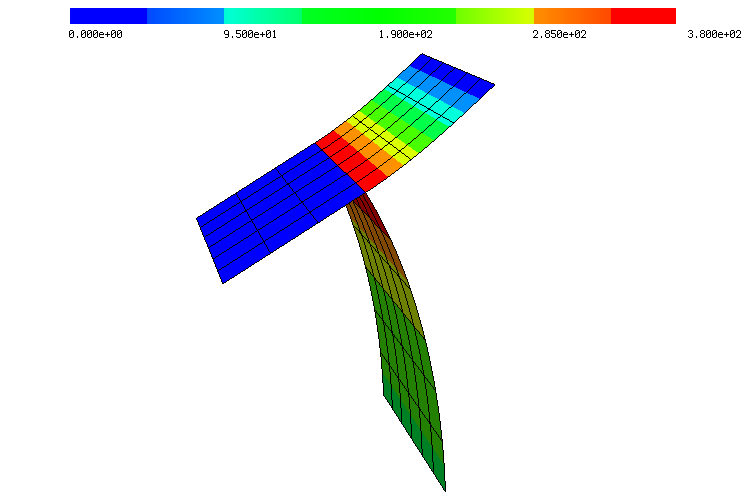A cantilever beam under a bending moment rolling up and a T-cantilever under a shear force (modulus of the bending tensor displayed).

Interpolating the membrane strain fields into so-called Regge finite elements led to a generally applicable method to avoid membrane locking [2021].

Displacement error with respect to the number of elements of a shell for different thicknesses. Left: Locking. Right: No locking with Regge interpolation.

Recently, we investigated the Babuška or plate paradox, where convergence fails when a domain with curved boundary is approximated by polygonal domains in linear bending problems with simple support boundary conditions. We showed that the paradox also occurs for a nonlinear bending-folding model which enforces vanishing Gaussian curvature, and it can be cured by cutting the interface edges [2025].

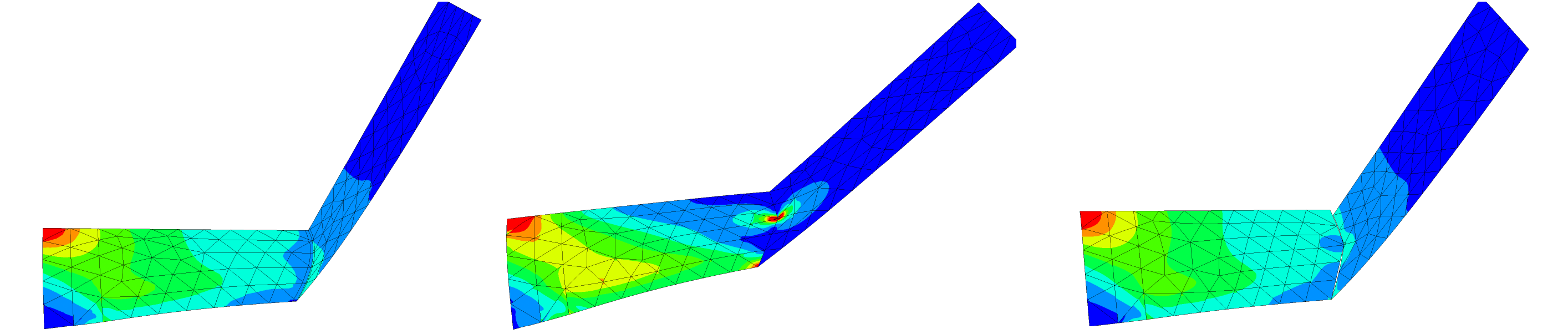Babuška paradox in an experiment (top) and simulation (bottom, the modulus of the bending stress is displayed).

In many applications, thin shell-like structures are integrated within or attached to volumetric bodies. This includes reinforcements placed in soft matrix material in lightweight structure design, or hollow structures partially or completely filled. We successfully coupled our shell method with nonlinear solid mechanics to simulate such structures in an efficient and locking-free manner [2025].