Research activities

In several applications, such as shells, general relativity, geometric flows, and cell membranes, the curvature of surfaces and Riemannian manifolds plays a fundamental role. In discrete differential geometry (DDG), algorithms to approximate curvature quantities of discretized domains have been intensively investigated. Many of these procedures rely on computing angles, such as the dihedral angle to approximate the shape operator on polyhedral surfaces or the angle defect for the Gauss curvature of surfaces and two-dimensional Riemannian manifolds. Rigorous convergence analysis and extension to high-order methods can be difficult or unfeasible in this setting. By embedding DDG into a FEM context, rigorous numerical analysis tools become available to investigate and extend those algorithms. To this end, so-called distributional finite elements are essential. They entail weak regularity such that differential operators must be understood in the sense of distributions.

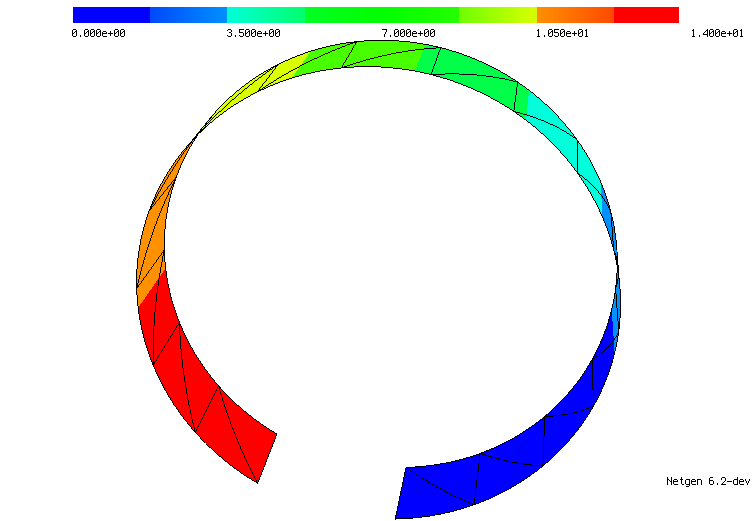
For intrinsic curvatures of (pseudo-)Riemannian manifolds with corresponding metric tensor, the question arises for a given approximation of a metric tensor, how close is the discrete curvature to the exact one? Moreover, how to define the nonlinear curvature on such a discrete metric, which is, in general, non-smooth. It turned out that Regge finite elements are the appropriate space to approximate metrics. They are symmetric, matrix-valued, and only their tangential-tangential components are continuous over element interfaces. We were able to define and analyze the Gauss curvature for 2D manifolds [2023, 2024], the scalar curvature for arbitrary dimensional manifolds [2024], the Einstein tensor [2025] (for arbitrary dimension), and recently the full Riemann curvature tensor in any dimension [2024], which is a fourth-order tensor encoding all intrinsic curvature information of a (pseudo-)Riemannian manifold. Future applications include geometric flows and especially numerical relativity, solving the Einstein field equations of general relativity. We successfully used the Regge elements to construct a simple and general method to avoid membrane locking in nonlinear shells.

NGSolve add-on package for differential geometry support, especially for Riemannian manifolds: NGSDiffGeo.

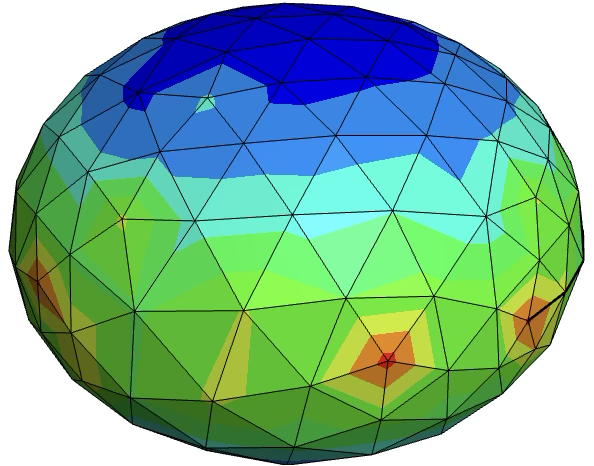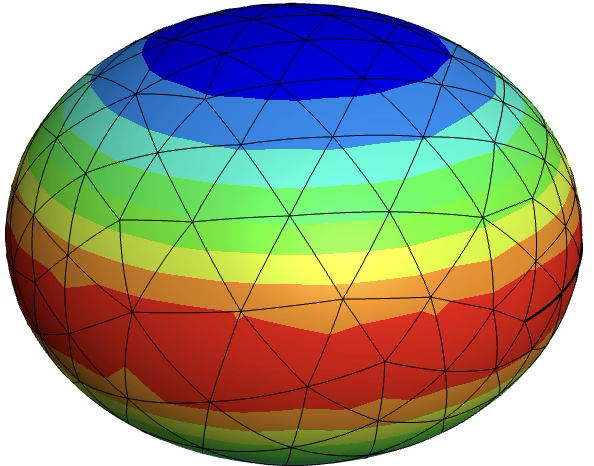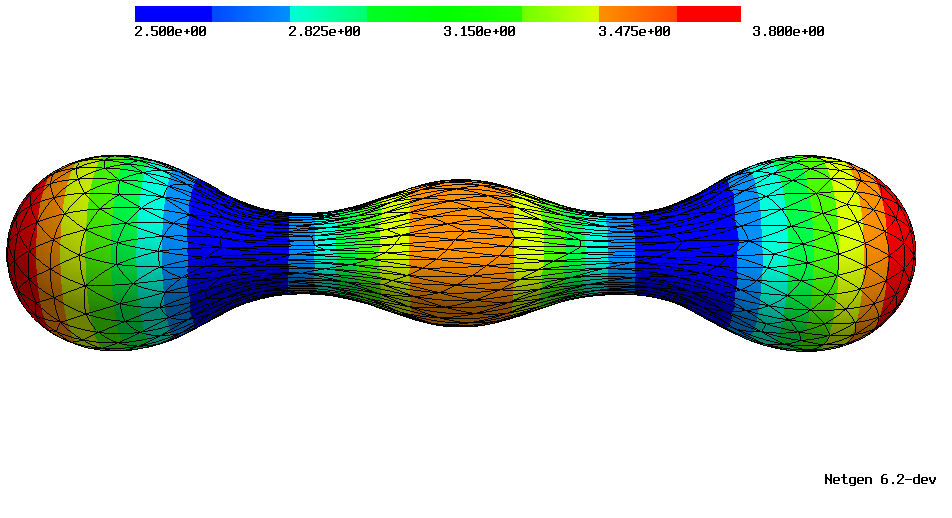
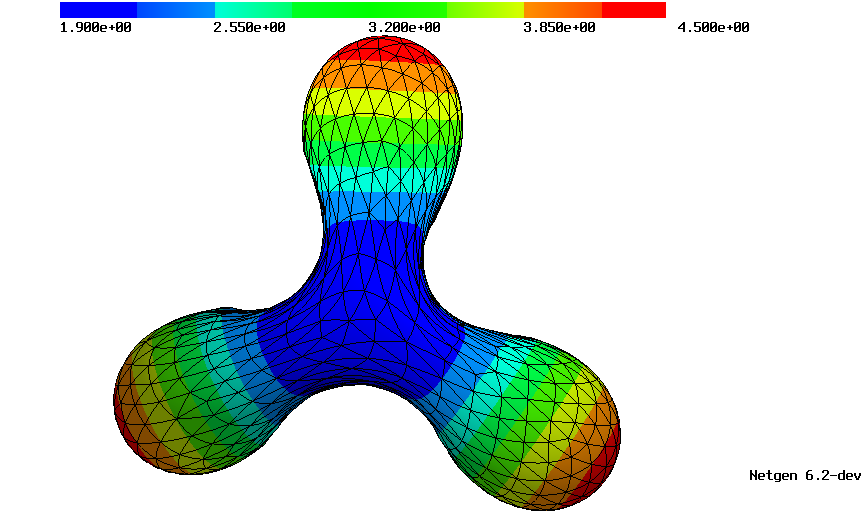
Approximated Gauss curvature on a polyhedral surface and a surface with quadratically curved elements.

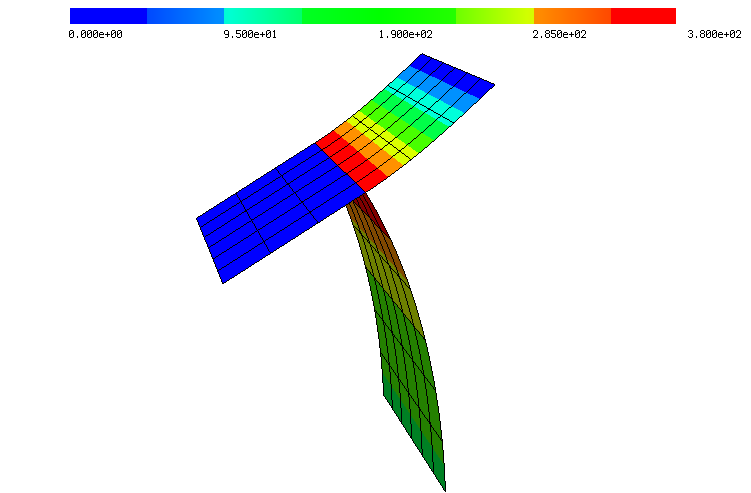
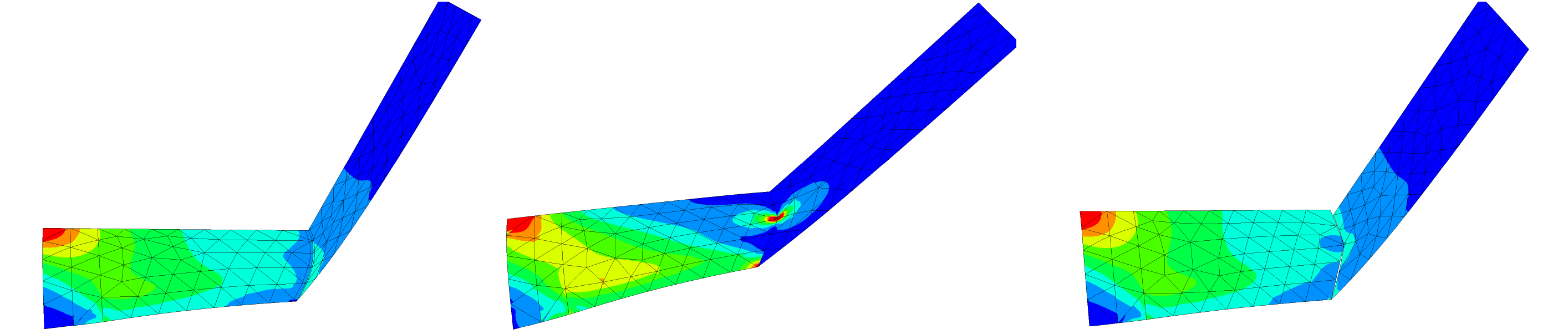
We extended the concept of the dihedral angle from DDG to approximate the shape operator (Weingarten tensor) on an arbitrarily approximated surface embedded in \(\mathbb{R}^3\). The distributional shape operator acts on Hellan–Herrmann–Johnson finite elements as test functions. We successfully applied the distributional shape operator to compute the curvature of cell membranes and for the bending term of nonlinear shells. A rigorous numerical analysis and convergence is a work in progress.

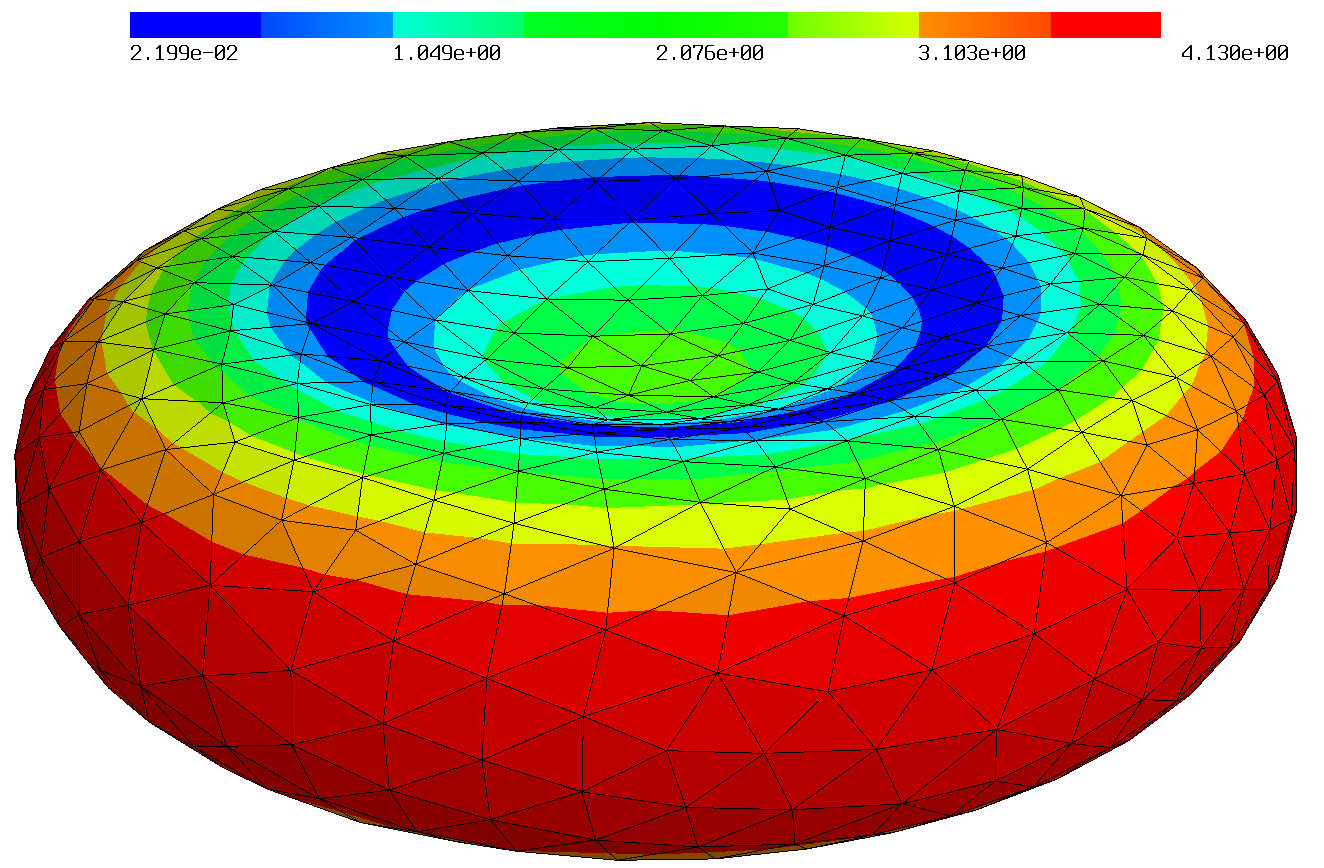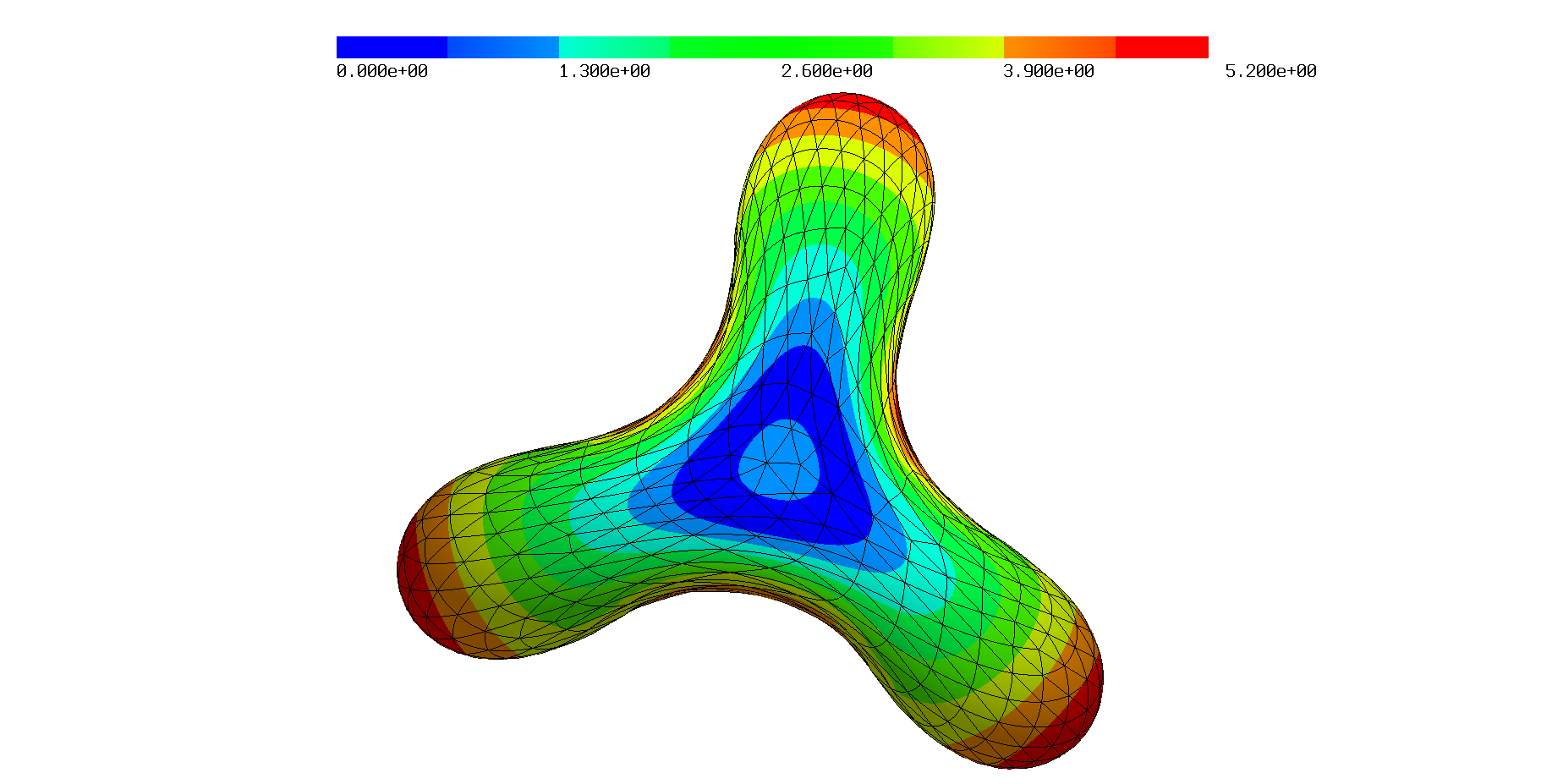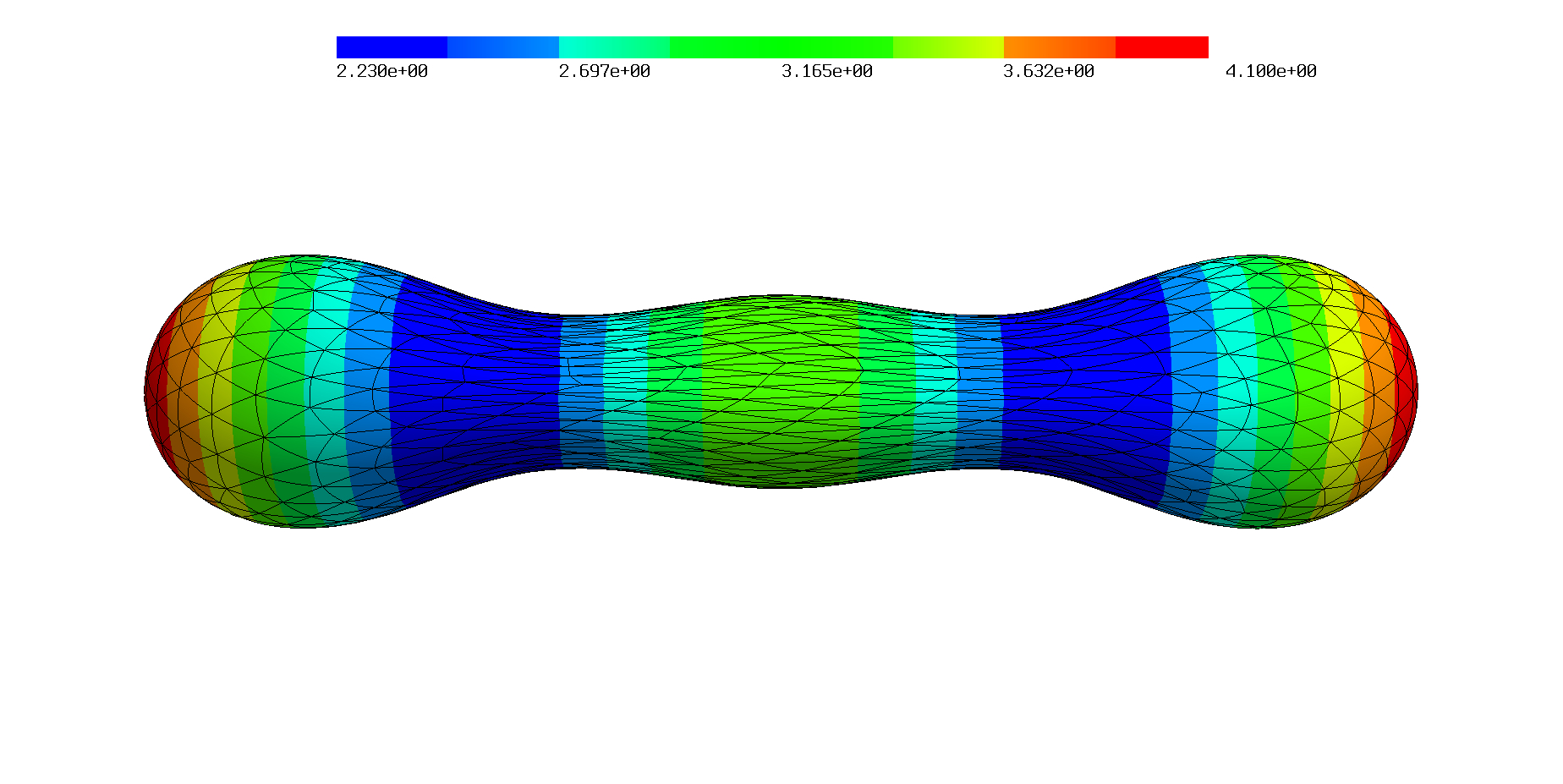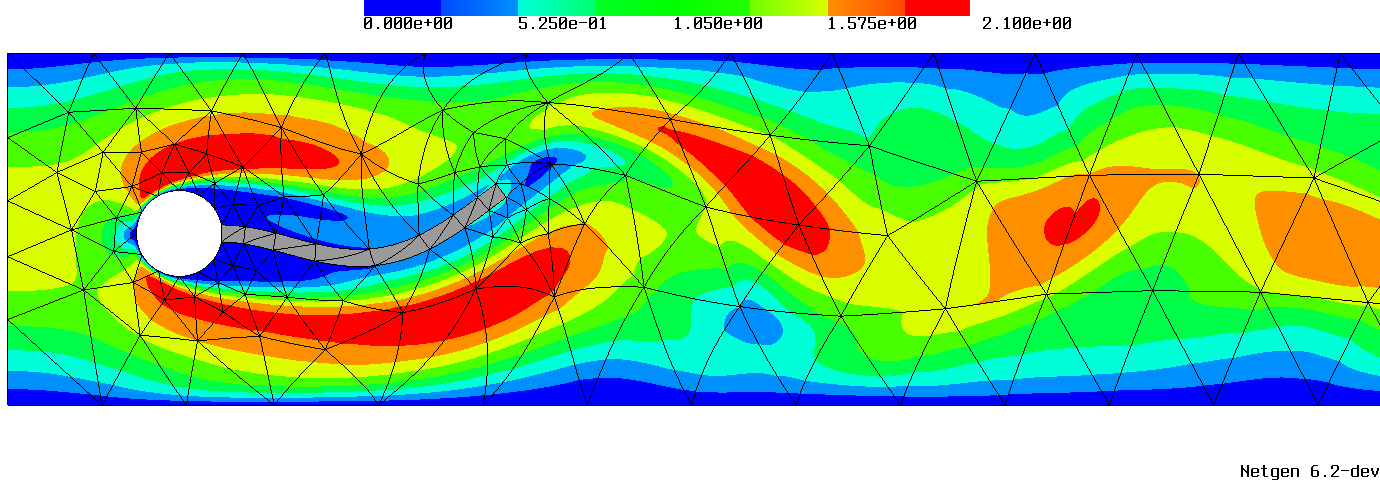
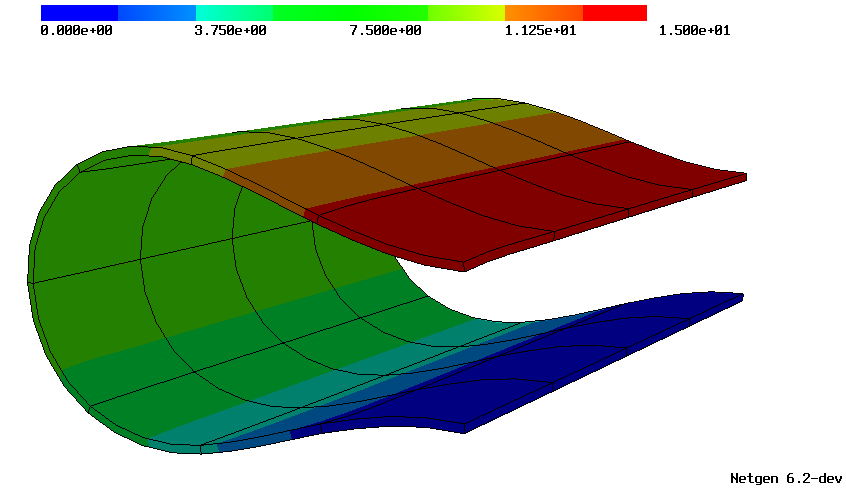
Mean curvature on quadratically curved surfaces.

To simulate thin-walled structures, where one direction is significantly smaller than the others, a dimension reduction leads to surface shell equations. Shells have a wide range of industrial applications and are an active research field. Their numerical solution with the finite element method is essential. Motivated by discrete differential geometry we used a distributional Weingarten tensor acting on Hellan–Herrmann–Johnson finite elements, we developed locking-free mixed finite element methods for nonlinear Koiter shells [2019, 2021, 2024] and extended the tangential-displacement and normal-normal stress continuous (TDNNS) method from linear Reissner–Mindlin plates to nonlinear Naghdi shells [2024]. With the structure-preserving finite elements, our methods can handle non-smooth shell structures such as kinked and branched shells.

A cantilever beam under a bending moment rolling up and a T-cantilever under a shear force (modulus of the bending tensor displayed).

Interpolating the membrane strain fields into so-called Regge finite elements led to a generally applicable method to avoid membrane locking [2021].

Displacement error with respect to the number of elements of a shell for different thicknesses. Left: Locking. Right: No locking with Regge interpolation.

Recently, we investigated the Babuška or plate paradox, where convergence fails when a domain with curved boundary is approximated by polygonal domains in linear bending problems with simple support boundary conditions. We showed that the paradox also occurs for a nonlinear bending-folding model which enforces vanishing Gaussian curvature, and it can be cured by cutting the interface edges [2025].

Babuška paradox in an experiment (top) and simulation (bottom, the modulus of the bending stress is displayed).

In many applications, thin shell-like structures are integrated within or attached to volumetric bodies. This includes reinforcements placed in soft matrix material in lightweight structure design, or hollow structures partially or completely filled. We successfully coupled our shell method with nonlinear solid mechanics to simulate such structures in an efficient and locking-free manner [2025].

Recently, metamaterials have attracted massive attention in industry and academia. These artificially produced objects have physical properties not present in naturally occurring materials and have applications in several fields, such as biomedicine and stealth technology. More than standard elasticity models are required to discretize these hand-made materials and complicated real-life materials such as bones. The arising models incorporate additional length scales and fields. Examples are Cosserat elasticity and the (relaxed) micromorphic continua. The extra parameters and fields lead to potential locking behaviour. We constructed and analyzed stable mixed methods for the relaxed micromorphic model [2021, 2022, 2024, 2025]. In Cosserat elasticity, the limit process when the coupling constant tends to infinity leads to the couple stress problem, commonly used to model generalized materials. We presented and analyzed parameter-robust mixed methods for linear Cosserat elasticity combining the mass-conserving mixed stress (MCS) and tangential-displacement and normal-normal stress continuous (TDNNS) methods [2024].

In several problems in industry and medicine, including the optimal design of aircraft, electric motors, or electric impedance tomography, an optimal shape with respect to a given objective function under constraints is searched for. Shape optimization problems involve the shape derivative of possibly lengthy and complicated expressions. We implemented an automated shape differentiation tool in the open-source finite element software NGSolve, enabling shape gradient and shape Newton methods without the need to compute the shape derivative by hand [2021]. In addition, this makes using non-Lagrangian finite elements in shape optimization problems more attractive, where additional space-dependent transformation rules have to be differentiated.

Initial and optimized geometry of a cantilever under vertical force on the right side using a St. Venant–Kirchhoff model in nonlinear elasticity.

We have successfully applied this framework to minimize the Canham–Helfrich–Evans (CHE) bending energy in the context of cell membranes [2023]. The method used to reduce the fourth-order problem to a mixed second-order problem turned out to be fruitful in combination with the theory of shape optimization.

Two solutions of the CHE energy with different nonzero spontaneous curvatures. Colors indicate the modulus of the mean curvature of the shapes.

The interaction between fluids and solids can be demanding due to the permanent change of the material domains. We investigated Arbitrary Lagrangian-Eulerian (ALE) methods, where the fluid velocity gets discretized by exactly divergence-free finite elements. We derived a method where the incompressibility constraint is exactly fulfilled for moving domains [2017, 2021].

For anisotropic physical structures, shear locking can be observed in the finite element discretization of (nonlinear) elasticity. The tangential displacement and normal-normal-stress continuous (TDNNS) method has elegantly circumvented this behaviour in linear elasticity. Besides the displacement, the stress tensor is introduced as an additional variable. The stress and displacement fields are discretized by matrix- and vector-valued finite elements, where only specific components are continuous. Extending this mixed method to the finite strain regime turned out to be challenging as, on the one hand, this two-field formulation would require inverting the nonlinear stress-strain relation, and on the other hand, the displacement’s weak regularity leads to a distributional gradient, which cannot be multiplied in general. We were able to solve this problem in terms of a three-field Hu–Washizu formulation by computing a discrete \(L^2\) Riesz representative of the distributional deformation gradient as a third field [2021, 2021]. The resulting method extends the robustness property concerning shear locking to the nonlinear regime.

Real-life materials cannot be indefinitely deformed without damaging them. Plasticity involves irreversible deformations, and damage weakens the material structure. We investigated a novel finite-strain model including plasticity and damage in two and three spatial dimensions numerically and theoretically [2021].

Rubber-like materials entail difficulties in numerical simulations due to their (nearly) incompressible character. We investigated under which boundary conditions a divergence-free displacement can be determined independently from the pressure reaction in incompressible linear elasticity. If not possible, we derived conditions under which it is possible to determine the displacement pressure robustly, i.e. pollution-free from the pressure reaction [2023]. The mass-converging mixed stress (MCS) method has been developed to simulate the (Navier-)Stokes equations in a pressure robust manner. It can be readily adapted to solve (nearly) incompressible linear elasticity problems. However, similar to the TDNNS method, it relies on the inversion of the material law. This makes incompressible finite elasticity unfeasible. We used a three-field Hu–Washizu formulation and a stabilization motivated by hybrid Discontinuous Galerkin (HDG) methods to successfully extend the MCS method to the nonlinear regime by adding the deformation gradient as an additional strain unknown [2025].